 |
||||
|
Programmeermethoden 2018
Vierde programmeeropgave: Othello
De vierde programmeeropgave van het vak
Programmeermethoden
in het najaar van 2018
heet Othello;
zie ook het
elfde werkcollege,
en lees geregeld deze pagina op WWW.
Spreekuur in zalen 302 ... 309: donderdag 15, maandag 19, donderdag 22, maandag 26, donderdag 29 november, maandag 3, donderdag 6 en maandag 10 december 2018, van circa 15:15 tot 17:00 uur.
De opgave
Het is de bedoeling om een C++-programma te maken dat de gebruiker
in staat stelt het spel Othello (zie ook Reversi) te spelen via een eenvoudig menu.
Othello-borden worden in het C++-programma gerepresenteerd door ingewikkelde pointer-structuren. Het is de bedoeling een klasse OthelloBord te maken, die onder meer memberfuncties heeft als afdrukken, menszet en computerzet. Uiteraard heeft deze klasse ook een constructor en een destructor. Verder moeten gedane zetten met behulp van een stapel ongedaan gemaakt kunnen worden, en kan het aantal vervolgpartijen worden uitgerekendi (als je deze twee mogelijkheden niet hebt kost dat een punt).
Het "normale" spel Othello gaat als volgt.
Op een 8 bij 8 bord wordt gespeeld met schijfjes die
aan de ene kant wit en aan de andere kant zwart (of rood) zijn.
Om de beurt leggen de spelers, wit W en zwart
Z geheten,
een schijfje met hun eigen kleur naar boven
op een nog leeg vakje.
Dit mag alleen op een plek zodat stenen van de tegenstander
geslagen worden.
Stenen van de tegenstander die ingesloten raken, hetzij horizontaal, of
verticaal, of diagonaal, tussen eigen stenen, worden geslagen:
ze worden omgekeerd, en krijgen dus de eigen kleur;
dit geldt ook voor meerdere stenen.
Zwart begint.
Als een speler niet kan zetten, moet hij/zij passen.
Het spel is afgelopen als geen van de spelers
meer kan zetten, bijvoorbeeld als het bord vol is.
Wij maken het iets eenvoudiger:
als een speler niet kan, terwijl het bord niet vol is,
heeft hij/zij meteen verloren.
Winnaar is degene met de meeste stenen in zijn of haar kleur;
gelijk spel is mogelijk;
in dit geval win je met "het verschil in aantal stenen".
Voor de vierde programmeeropgave hoeft het niet grafisch
(net als in de voorbeeld-standen hier onder),
en het programma hoeft niet zo goed te spelen!
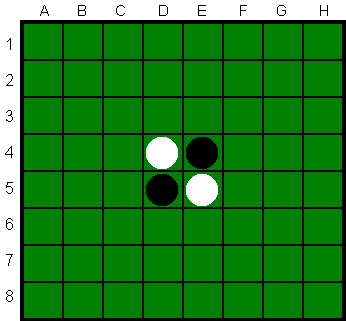
De beginconfiguratie voor Othello staat links hieronder
(en ook in het plaatje rechtsboven; voor Reversi is deze overigens iets anders),
gevolgd door enkele voorbeeldzetten:
. . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . .
. . . W Z . . . . . . W Z . . . . . . W Z . . .
. . . Z W . . . . . . Z Z Z . . . . . Z W Z . .
. . . . . . . . . . . . . . . . . . . . . W . .
. . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . .
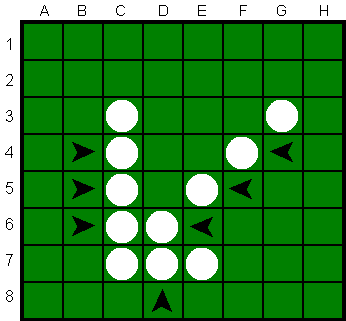
In één zet kunnen stenen uit verschillende richtingen tegelijk
geslagen worden. De stenen moeten echt aan beide zijden
ingesloten raken om geslagen te worden. In een richting
kunnen meerdere stenen tegelijk geslagen worden.
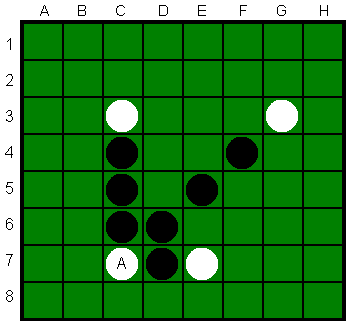
Op de kleurenplaatjes (van www.othello.nl)
worden bij het zetten op plek A (positie C7) zeven schijven van zwart omgedraaid.
We spelen het spel met aangepaste regels.
Allereerst mag gekzoen of Zwart een mens of een computer is,
en daarna of Wit een mens of een computer is.
Het moet ook mogelijk zijn de computer tegen zichzelf te laten spelen.
Daarna mag ook de grootte van het bord gekozen worden:
het aantal rijen m en het aantal kolommen n,
beide minstens 2, en even.
Normaal geldt dus dat m=8 en n=8.
De vier beginschijven staan in het midden.
Als de speler aan zet is, wordt de stand, in eenvoudig
formaat, op het scherm
getoond, en kan de speler zijn/haar zet doen, of juist de laatste
eigen zet
(en meteen de tussenliggende computerzet) terugnemen,
of het aantal mogelijke vervolgpartijen voor de huidige stand laten
uitrekenen.
De mogelijke zetten worden zo mogelijk opgesomd
(bijvoorbeeld als 1: C2, 2: F5, 3: A8)
zodat de speler eenvoudig kan kiezen; het
invoeren van coördinaten is ook goed.
De door de speler uitgekozen zet wordt gedaan, waarna
(bijvoorbeeld) de computer een
willekeurige (gebruik een randomgenerator, bijvoorbeeld
rand ( )), maar uiteraard wel toegestane, zet doet.
Liefhebbers mogen natuurlijk hun eigen creativiteit inzetten,
door bijvoorbeeld de computerzet waarbij de meeste stenen geslagen
worden te kiezen (wat overigens niet altijd het beste is).
Schrijf een functie voor de klasse OthelloBord die een pointerstructuur aanlegt, waarbij ieder vakje, naast bijvoorbeeld een char als inhoud, tevens een array met 8 pointers naar de onmiddellijke buren heeft: linksboven, middenboven, rechtsboven, rechts, rechtsonder, middenonder, linksonder en links. De vakjes aan de randen bevatten uiteraard diverse NULL-pointers. Het bord is dus niet een m bij n array, maar een zeer ingewikkelde pointerstructuur.
Alle tussenstanden moeten op een stapel worden bijgehouden, en spelerzetten kunnen daarmee zelfs herhaald teruggenomen worden. Hiertoe moeten dus alle standen (en niet de zetten) worden onthouden, of liever gezegd: zodra de speler zet, wordt de oude stand (het complete bord) opgeslagen. Er moet dus een memberfunctie kopieer gemaakt worden, die de gehele pointerstructuur kopieert! Dit onderdeel is zeker niet eenvoudig; mocht het ontbreken, dan kost dat een halve punt.
Verder dient er een recursieve memberfunctie vervolg geschreven te worden die gegeven een zekere stand het totale aantal mogelijke vervolgpartijen, dat overigens erg groot kan zijn, uitrekent. Hiervoor moeten alle mogelijke zetten van beide spelers doorgerekend worden. Dit onderdeel is zeker niet eenvoudig; mocht het ontbreken, dan kost dat een halve punt.
Het is de bedoeling om minimaal een drietal files te produceren:
de eerste bevat main en het menu,
de tweede (zeg othello.h) bevat de klasse-definitie van het Othello-bord,
en de derde (zeg othello.cc) bevat de functies uit die klasse.
Daarbij komen wellicht nog files stapel.h en stapel.cc.
Maak ook een makefile.
Maak bij voorkeur gebruik te maken van de volgende
voorbeeldfiles, van waaruit de opgave stap voor stap kan worden gedaan.
Je kunt ook je eigen files met andere functies maken, maar gesplitst moet er worden.
De files zijn:
- File met main: hoofd.cc.
- Headerfile met klassen: othellobord.h.
- Bijbehorende C++-file: othellobord.cc.
- En de bijpassende makefile (let op de TABs).
Opmerkingen
Gebruik geschikte (member)functies.
Bij deze opgave mogen wederom bij
elke functie (zelfs main) tussen begin-{ en
eind-} hooguit circa 30 niet al te volle regels staan!
Elke functie dient van commentaar voorzien te zijn.
Let op goed parametergebruik: alle parameters, met uitzondering van membervariabelen, in de heading doorgeven, en de
variabele-declaraties zowel bij main als bij de
andere functies aan het begin.
De enige te gebruiken headerfiles zijn in principe
iostream, cstdlib en ctime
(voor de random-generator).
Zeer ruwe indicatie voor de lengte van de gezamenlijke C++-files: 500 regels.
Denk aan het infoblokje.
Een vier-weken-schema:
- week 1: pointerpracticum, lezen opgave, files klaar maken, begin pointerbord
- week 2: pointerbord af, zetten, computerspeler
- week 3: spel helemaal in orde; stapel
- week 4: vervolgpartijen, experiment, verslag
Uiterste inleverdatum: maandag 10 december 2018, 17:00 uur.
Manier van inleveren:
- Digitaal de C++-code
inleveren: stuur een email naar
pm@liacs.leidenuniv.nl.
Stuur geen executable's, lever alleen de C++-files en de makefile digitaal in! Noem de file othelllo.cc hier bij voorkeur zoiets als garfunkelsimonothello4.cc, dit voor de opdracht van het duo Simon-Garfunkel, en analoog de andere files. Zorg dat de makefile werkt met de gebruikte filenamen! De laatst voor de deadline ingeleverde versie wordt nagekeken. - En ook een papieren versie van het verslag
(inclusief de C++-code van alle files, en de makefile) deponeren
in de speciaal daarvoor bestemde doos "Programmeermethoden"
bij kamer 159 van het Snellius-gebouw.
Overal duidelijk datum en namen van de (maximaal twee) makers vermelden, in het bijzonder als commentaar in de eerste regels van de C++-code.
Het verslag (uiteraard weer in LaTeX, zie de eerdere opgaven) moet het volgende bevatten: een zeer korte beschrijving van het programma, een beschrijving van punten waarop het programma faalt (indien van toepassing), en een tabel met gewerkte uren, uitgesplitst per week en per persoon. En uitleg en een referentie betreffende Othello, en een over computers en Othello. En tekst en een of meer grafiekjes (zie het bijbehorende werkcollege) die een experiment met Othello illustreren. Speel flinke aantallen spelletjes (wie wint er? na hoeveel zetten? met hoeveel punten?), en geef zo mogelijk enkele aantallen vervolgpartijen.
