Hendrik Jan Hoogeboom (Leiden NL)
The Algebra of Ciliates
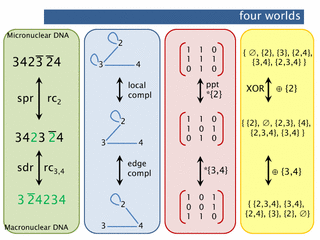
abstract. Ciliates, an ancient group of unicellular organisms, transform genes from their micronuclear (storage) form into their macronuclear (expressible) form. This process is called gene assembly. The DNA processing involved is interesting from both the biological and the computational point of view.There are various equivalent ways to formally model gene assembly (at the level of genes). Two of these were extensively studied in the book «Computation in living cells: gene assembly in ciliates» by Ehrenfeucht, Harju et al (Springer, 2004). However, one additional viewpoint is particularly enlightening: the process may be seen as (partial) matrix inversion. We show that on the one hand this leads to a number of significant consequences for the model and on the other hand it enriches general theory.
Turku, Unconventional Computation UC2011, Workshop on Language Theory in Biocomputing, 9 June 2011. (invited) (presentation)
Tampa, 1079th AMS Meeting, special session on Discrete Models in Molecular Biology, 10 march 2012. (slightly more math than version above) (presentation)
Hasselt, DNA Computing & Molecular Programming Symposium, 15 May 2013

References
- R. Brijder, H.J. Hoogeboom. The Algebra of Gene Assembly in Ciliates. In: Discrete and Topological Models in Molecular Biology», Jonoska and Saito, eds, Natural Computing Series, Springer (2014) 289-307. doi: 10.1007/978-3-642-40193-0_13
Background
Prescott, D.: Genome gymnastics: Unique modes of DNA evolution and processing in ciliates. Nature Reviews 1 (2000) 191-199. doi: 10.1038/35042057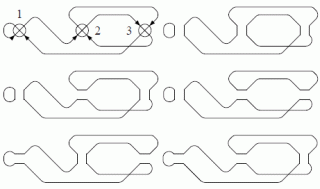
Graph Polynomials
CiE 2014 (Computability in Europe) Budapest, Hungary, June 23-27, 2014. Special Session on Bio-inspired Computation. (presentation)"Graph polynomials motivated by Gene Assembly", Math colloquium University South Florida, Tampa, 29 Jan 2016. (presentation). Also Math colloquium UNF, Jacksonville.
- Robert Brijder, Hendrik Jan Hoogeboom, Nataša Jonoska and Masahico Saito: Graphs Associated With DNA Rearrangements and Their Polynomials. Algebraic and Combinatorial Computational Biology» (R. Robeva, M. Macauley, eds.), Mathematics in Science and Engineering, Academic Press, 2019.
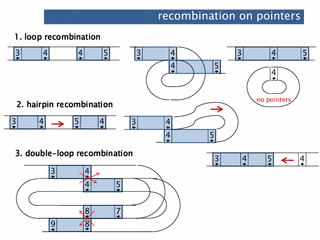
abstract. DNA rearrangement is a process often found in biology on both developmental and evolutionary scale. While many models have considered abstract operations involved in the rearrangement, the process itself can be directly modeled through four-regular graphs, as presented here. We describe ways to explain DNA rearrangements through four-regular graphs and double occurrence words. These models are illustrated through the rearrangement processes in a well-studied ciliate species where DNA recombination is observed on a massive scale. The number of resulting molecules and the intermediate molecules throughout this process can be counted as terms in graph polynomials, closely related to the well-known Tutte polynomial. We present two such polynomials in the last section. Keywords: DNA recombination, Ciliates, Four-regular graphs, Double occurrence words, Eulerian circuits, Graph polynomials
- R. Brijder, H.J. Hoogeboom: Graph Polynomials Motivated by Gene Rearrangements in Ciliates. A. Beckmann, E. Csuhaj-Varjú, and K. Meer (Eds.): CiE 2014, LNCS 8493, pp. 63-72, 2014. doi: 10.1007/978-3-319-08019-2_7
abstract. Gene rearrangements within the process of gene assembly in ciliates can be represented using a 4-regular graph. Based on this observation, Burns et al. [Discrete Appl. Math., 2013] propose a graph polynomial abstracting basic features of the assembly process, like the number of segments excised. We show that this assembly polynomial is essentially (i) a single variable case of the transition polynomial by Jaeger and (ii) a special case of the bracket polynomial introduced for simple graphs by Traldi and Zulli.
Interlace polynomials
- R. Brijder, H.J. Hoogeboom: Interlace polynomials for multimatroids and delta-matroids. European Journal of Combinatorics, Volume 40, August 2014, Pages 142-167. doi: 10.1016/j.ejc.2014.03.005 [arXiv:1010.4678] Erratum
abstract. We provide a unified framework in which the interlace polynomial and several related graph polynomials are defined more generally for multimatroids and delta-matroids. Using combinatorial properties of multimatroids rather than graph-theoretical arguments, we find that various known results about these polynomials, including their recursive relations, are both more efficiently and more generally obtained. In addition, we obtain several interrelationships and results for polynomials on multimatroids and delta-matroids that correspond to new interrelationships and results for the corresponding graph polynomials. As a tool we prove the equivalence of tight 3-matroids and delta-matroids closed under the operations of twist and loop complementation, called vf-safe delta-matroids. This result is of independent interest and related to the equivalence between tight 2-matroids and even delta-matroids observed by Bouchet.
- R. Brijder and H.J. Hoogeboom: The Interlace Polynomial and the Tutte-Martin Polynomial. Submitted for the CRC Handbook on the Tutte Polynomial edited by J. Ellis-Monaghan and I. Moffatt.
Introduction. The interlace polynomial was discovered by Arratia, Bollobás, and Sorkin by studying DNA sequencing methods. Its definition can be traced from 4-regular graphs (or 2-in, 2-out digraphs), to circle graphs and finally to arbitrary graphs (multiple edges are not allowed). We take the same route. In Section 2 we consider the theory of circuit partitions in 4-regular graphs as initiated by the seminal paper of Kotzig, and consider the Martin polynomial for 4-regular graphs (and 2-in, 2-out digraphs), which counts, for any k, the number ak of circuit partitions of cardinality k. In Section 3 we associate a circle graph to any Eulerian circuit of a 4-regular graph, and we invoke a theorem by Cohn-Lempel-Traldi to recover ak from its circle graph. This leads naturally to the definition of the interlace polynomial for arbitrary graphs. [...]
London, Royal Holloway University of London, Workshop on New Directions for the Tutte Polynomial: Extensions, Interrelations, and Applications, 11th-14th July 2015. (abstract) (presentation)
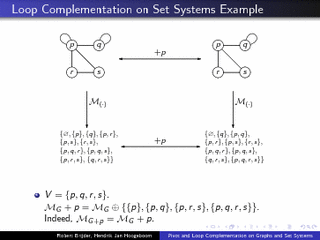
Pivot and Loop Complementation on Graphs and Set Systems
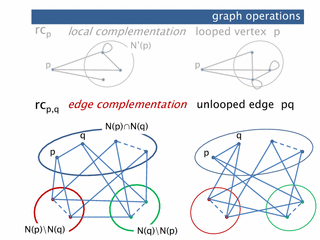
Prague, Theory and Applications of Models of Computation TAMC2010. (presentation)abstract. We study the interplay between principal pivot transform (pivot) and loop complementation for graphs. This is done by generalizing loop complementation (in addition to pivot) to set systems. We show that the operations together, when restricted to single vertices, form the permutation group S 3. This leads, e.g., to a normal form for sequences of pivots and loop complementation on graphs. The results have consequences for the operations of local complementation and edge complementation on simple graphs: an alternative proof of a classic result involving local and edge complementation is obtained, and the effect of sequences of local complementations on simple graphs is characterized.
References
-
R. Brijder, H.J. Hoogeboom.
The Group Structure of Pivot and Loop Complementation on Graphs and Set Systems.
European Journal of Combinatorics 32 (2011) 1353-1367.
doi: 10.1016/j.ejc.2011.03.002
[arXiv:0909.4004]
also: Pivot and Loop Complementation on Graphs and Set Systems, TAMC 2010, LNCS 6108 (2010) 151-162, doi: 10.1007/978-3-642-13562-0_15 - R. Brijder, H.J. Hoogeboom. Maximal Pivots on Graphs with an Application to Gene Assembly. Discr.Appl.Math. 158 (2010) 1977-1985. doi: 10.1016/j.dam.2010.08.030
- R. Brijder, H.J. Hoogeboom. Reality-and-Desire in Ciliates. In: Algorithmic Bioprocesses (Condon etal, eds.), Natural Computing Series, Springer (2009) pp.99-115.
- R. Brijder, T. Harju, H.J. Hoogeboom, Pivots, determinants, and perfect matchings of graphs Theor. Comp. Sci. 454 (2012) 64-71. doi: 10.1016/j.tcs.2012.02.031" From: [arXiv:0811.3500] (2008)
- R.Brijder, M.Daley, T.Harju, N.Jonoska, I.Petre, G.Rozenberg: Computational nature of gene assembly in ciliates. In: Rozenberg, Bäck, Kok, eds.: Handbook of Natural Computing. Volume 3. Springer (2012) 1233-1280.
Background
A. Ehrenfeucht, T. Harju, I. Petre, D. Prescott, G. Rozenberg, Computation in Living Cells: Gene Assembly in Ciliates, Natural Computing Series, Springer (2004)Greslin, Prescott etal. Reordering of nine exons is necessary to form a functional actin gene in Oxytrichanova. PNAS 86, 6264-6268, Aug 1989.