LIACS >Kristian Rietveld >Courses >Programmeermethoden NA, Najaar 2017
headerimg

Banner image by Sebastian Niedlich on Flickr, CC BY-NC-SA 2.0

Programmeermethoden NA 2017
Derde programmeeropgave: 2-in-1

De derde programmeeropgave van het vak Programmeermethoden NA in het najaar van 2017 heet 2-in-1.

De meest recente versie van deze opdracht (met eventuele aanvullingen en verbeteringen) is altijd te vinden op: http://liacs.leidenuniv.nl/~rietveldkfd/courses/prna2017/opdr3.html. Dit is versie 12nov2017.

Er is ook een printer-vriendelijke versie: http://liacs.leidenuniv.nl/~rietveldkfd/courses/prna2017/opdr3.pdf.

Deze laatste programmeeropdracht staat geheel in het teken van het leren werken met NumPy en Matplotlib. De opdracht bestaat uit twee componenten, die worden aangestuurd via een menu-systeem. De twee componenten zijn Mini Game of Life en Angry Birds, en worden hieronder verder uitgelegd.

Het programma start zoals altijd met het weergeven van het infoblokje (en vergeet ook het commentaar bovenaan het programma niet!). Daarna volgt een menu met drie keuzes: Game of Life, Angry Birds of afsluiten. Schrijf een handige, generieke functie die de gebruiker vraagt een keuze in te voeren als geheel getal (in dit geval 1 t/m 3, maar maak hier parameters voor), deze omzet naar een int en controleert of de invoer een geldige keuze is. In het geval geen geheel getal of een ongeldige keuze was ingevoerd, laat dit de gebruiker weten en vraag opnieuw. De returnwaarde is de uiteindelijke, geldige keuze. We kunnen deze functie dan ook direct hergebruiken in de verschillende submenu's.

Belangrijk bij het implementeren van de menu's: roep vanuit een menu-functie niet telkens dezelfde menu-functie weer aan ("recursie") om de gebruiker opnieuw te vragen een optie te kiezen. Plaats de code voor het menu in plaats daarvan in een loop, die herhaaldelijk om menu-keuzes vraagt en deze afhandelt totdat het programma wordt afgesloten.

Bouw het programma op een gestructureerde en modulaire manier op. Maak gebruik van meerdere bestanden. Gebruik bijvoorbeeld drie bestanden: één voor Game of Life, één voor Angry Birds en een bestand met de hoofdfunctie (main), alle menus en aansturing. Dit laatste bestand is het hoofdbestand en zal import-regels bevatten voor functies en klassen uit de andere drie bestanden. Implementeer het infoblokje en alle menu's in het hoofdbestand. Roep na het maken van een menukeuze de juiste geimporteerde functies of methodes op een klasse aan.
Andere indelingen zijn natuurlijk ook goed, mits deze logisch zijn en minimaal uit 3 bestanden bestaan.

We verwachten boven ieder bestand een korte uitleg wat er allemaal in dat bestand is geïmplementeerd, en de namen en studentnummers van de auteurs. Zet bovenaan het hoofdbestand tevens in commentaar: de versie van de gebruikte interpreter, en versies van de NumPy en matplotlib modules (kan bijvoorbeeld worden opgevraagd met import numpy as np gevolgd door print np.__version__ en analoog voor matplotlib).

Mini Game of Life

In Mini Game of Life kan de gebruiker Life spelen via een menu-systeem. Het is de bedoeling dat het nummer van de huidige generatie, gevolgd door de Life-wereld wordt afgedrukt op het scherm en dat daaronder het menu staat op 1 regel. De menu-opties zijn genummerd en voor de invoer en controle van gekozen opties kan de functie worden gebruikt die we ook al voor het hoofdmenu hadden geschreven.

Van Wiki Life is een cellulaire automaat, in 1970 bedacht door John Horton Conway. Zie verder Wikipedia of hier. We gaan uit van een klein 2-dimensionaal rooster: 20 rijen bij 80 kolommen. We noemen dit de wereld en beginnen met een eindig aantal levende vakjes oftewel cellen. We slaan het rooster op als een twee-dimensionale NumPy-array met als data type bool. True duidt een levende cel aan, False een dode. Een levend vakje met minder dan 2 of meer dan 3 buren van de 8 (horizontaal, verticaal en diagonaal) gaat dood (uit eenzaamheid of juist overbevolking), met precies 2 of 3 levende buren overleeft het. In een dood vakje met precies 3 levende buren ontstaat leven. Dit leidt tot de volgende generatie. Let erop dat dit voor alle vakjes tegelijk gebeurt!

Eigenlijk moet het geheel zich afspelen op een oneindig rooster, maar we kiezen voor de eindige variant. Om moeilijkheden te voorkomen, spreken we af dat de rand van onze wereld altijd uit dode cellen blijft bestaan.

In het Life-menu zijn de volgende opties aanwezig:

  1. Stoppen. Life stoppen en teruggaan naar het hoofdmenu.
  2. Schoon. Maak de wereld leeg (alle cellen in de wereld gaan dood).
  3. Random. Maak de wereld schoon en vul deze met random dode en levende cellen.
  4. Glider. Vraag de gebruiker om coördinaten waar een Glider moet worden geplaatst. Controleer of voor deze coördinaten de Glider binnen de randen van de wereld valt. Zo nee, geef een foutmelding. Zo ja, plaats op die locatie een Glider in de wereld: 
    xx.
x.x
x..
  5. Een. Er wordt één generatie gedaan. Zet daarnaast op het scherm hoeveel cellen er zijn omgeklapt ten opzichte van de voorgaande generatie.
  6. Gaan. Er wordt een hele serie generaties (bijvoorbeeld 50 of misschien zelfs 300, maak zelf een keuze) gedaan — en allemaal achterelkaar getoond (zonder Enter's).

Voor de implementatie van Life is het verplicht gebruik te maken van object georiënteerd programmeren. We verwachten dat er een klasse (class) LifeWereld wordt gemaakt, met daarin onder meer functies (methoden) die ieder een operatie op de LifeWereld kunnen uitvoeren. In principe krijg je voor iedere menu-optie een methode in de klasse. Buiten de klasse LifeWereld is er een functie nodig om het spel aan te sturen. Hier wordt een klasse LifeWereld geïnstantieerd en daarna wordt er telkens gevraagd een menu-optie te kiezen. De gekozen menu-optie wordt afgehandeld door de juiste methode op het object aan te roepen. Bij Tips is enige inspiratie te vinden voor deze klasse.

Om de code flexibel te houden verwachten we in de klasse member-variabelen voor het volgende: het karakter te gebruiken voor het afdrukken van dode cellen, het karakter te gebruiken voor het afdrukken van levende cellen en het percentage levende cellen dat moet worden opgeleverd bij het random vullen van de wereld. Kies zelf redelijke standaardwaarden voor deze variabelen die je instelt in de __init__ methode.

Voor de liefhebbers: er zijn natuurlijke vele uitbreidingen mogelijk. Maak bijvoorbeeld een submenu waarin verschillende parameters kunnen worden ingesteld (zoals de karakters en het percentage hierboven). Je kunt ook een optie toevoegen om een Glidergun in de view te plaatsen. Of een veel grotere wereld ondersteunen en de mogelijkheid inbouwen om een view (het op het scherm zichtbare deel van de wereld) te verschuiven ... Maar vergeet niet eerst de rest van de opdracht te maken.

Angry Birds

In het Angry Birds component is het mogelijk Angry Birds te "spelen" door kogelbanen van afgeschoten vogels te plotten. Het spel kan worden gespeeld op verschillende planeten en er kunnen vogels worden afgevuurd met verschillende parameters. De data van de planeten en vogels moeten worden ingelezen uit bestanden. Voorbeelden zijn online beschikbaar: planeten.txt en vogels.txt. De datapunten per regel zijn gescheiden door tabs (hint: zie ook dictaat, hoofdstuk 9). Regels die beginnen met een # moeten worden beschouwd als commentaarregels en dienen te worden overgeslagen bij het inlezen. De gebruikte eenheden voor de datapunten vind je terug in de commentaarregel van elk bestand. Let erop dat je misschien de datapunten moet omrekenen naar een andere eenheid voor de rest van de opdracht. Het programma moet kunnen werken met een arbitrair aantal planeten en vogels.

Bij het starten van het spel wordt de gebruiker gevraagd of hij/zij gebruik wil maken van de data in de standaard bestanden vogels.txt en planeten.txt. Wanneer de gebruiker dit niet wil, dan wordt de gebruiker gevraagd om andere bestandsnamen op te geven. Vervolgens worden het planeten-bestand en vogels-bestand ingelezen, waarna het Angry Birds menu kan worden getoond. Indien tenminste één van de bestanden niet kan worden gelezen, wordt een nette melding op het scherm gezet en wordt er teruggekeerd naar het hoofdmenu.

In het Angry Birds menu krijgt de gebruiker de keuze uit twee experimenten en een optie om terug te keren naar het hoofdmenu:

  1. Het afvuren van alle volgens op een gekozen planeet.
  2. Het afvuren van één gekozen vogel op alle planeten.
  3. Afsluiten: terugkeren naar het hoofdmenu.
Afhankelijk van de keuze van het experiment, krijgt de gebruiker een genummerde lijst planeten of vogels te zien. De gebruiker krijgt de vraag een planeet of vogel te kiezen door het corresponderende nummer in te toetsen. Controleer ook dat dit nummer een geldige keuze is!

Hierna wordt de gebruiker gevraagd of de plot moet worden getoond op het scherm of moet worden opgeslagen in een bestand. In geval van de keuze voor een bestand moet ook om een bestandsnaam worden gevraagd. Laat de bestandsnaam eindigen met .pdf, zodat de plot als PDF-bestand wordt opgeslagen. Hierdoor kun je de opgeslagen plots direct gebruiken in je verslag.

Nu zijn alle gegevens compleet om het experiment uit te voeren en de verschillende kogelbanen te berekenen. Maak zoveel mogelijk gebruik van NumPy arrays en de eigenschappen hiervan! Schrijf voor natuurkundige formules die je gebruikt aparte functies (die opereren op NumPy arrays). Maak ook netjes de constanten aan. Gebruik duidelijke namen voor de functies en variabelen, niet g maar valversnelling. Merk op dat de data voor de twee verschillende experimenten op eenzelfde manier wordt berekend, schrijf bijvoorbeeld een generieke herbruikbare functie.

We gaan uit van het volgende:

  • Per planeet worden de massa van de planeet en de radius (de afstand van het middelpunt van de planeet tot de oppervlakte) gegeven. Met deze gegevens kan de valversnelling g worden berekend, welke geldt voor objecten vlakbij de oppervlakte van de planeet: g = GM ⁄ r2. Hiervoor hebben hiervoor de gravitatieconstante nodig: valversnelling = 6.67384 × 10-11 N ⋅ m2 ⁄ kg2
  • De vogels hebben geen last van de luchtweerstand en zijn in een vrije val. Per vogel is er een startsnelheid v0 en lanceerhoek θ0 opgegeven. De vogels worden gelanceerd vanaf een lanceerplatform dat zich op 10 meter van de oppervlakte van de planeet bevindt. Hierdoor gaan we ervan uit dat de vogels alleen versnelling ondervinden in de verticale richting (zwaartekracht). De zwaartekracht is een versnelling g die voor een specifieke planeet is berekend. Op basis hiervan kunnen we de volgende (vereenvoudigde) formules gebruiken:
    x - x0 = (v0 cos θ0)t
    y - y0 = (v0 sin θ0)t - 1⁄2gt2

    (x0, y0) is de startpositie van de kogel (de locatie van het lanceerplatform). Voor gegeven tijdstippen t kan met deze formules een locatie (x, y) worden berekend.

    Let op: np.cos verwacht radialen en geen graden. Om graden om te zetten naar radialen kun je gebruik maken van np.deg2rad.
  • Gebruik voor t een tijdspanne van 0 tot en met 30 seconden en genereer 100 tijdstappen (Hint: np.linspace). Bereken voor elk tijdstip de locaties (x, y) voor iedere vogel. Hierna kunnen alle banen worden geplot; markeer elk datapunt met een teken (bijvoorbeeld een stip) en zorg voor verbindende lijnen tussen de stippen. Vang de "handles" op zodat je later een legenda kunt maken.

    Opmerking: door slim gebruik te maken van NumPy arrays kun je de x-locaties voor alle vogels (of voor alle planeten) voor alle tijdstippen in 1 keer berekenen en hetzelfde voor de y-locaties. Je past dan dezelfde formule eenmaal toe op een array van N, M elementen.

Nadat alle punten zijn berekend kan de plot worden gegenereerd. Bepaal aan de hand van de berekende punten een goed bereik voor de x-as en de y-as, zodat de kogelbanen goed zichtbaar zijn. Denk bij de plot aan de titel, labels op de assen en legenda. Ook willen we graag een stippellijn y = 10 zien, dat de hoogte aangeeft waarvan de vogels zijn afgevuurd. Na het tonen of wegschrijven van de plot, wordt teruggekeerd naar het Angry Birds menu om te kijken of de gebruiker nog een experiment wil uitvoeren. Hieronder is een voorbeeldplot te zien, waarin de voorbeeldvogels zijn afgevuurd op planeet Aarde.

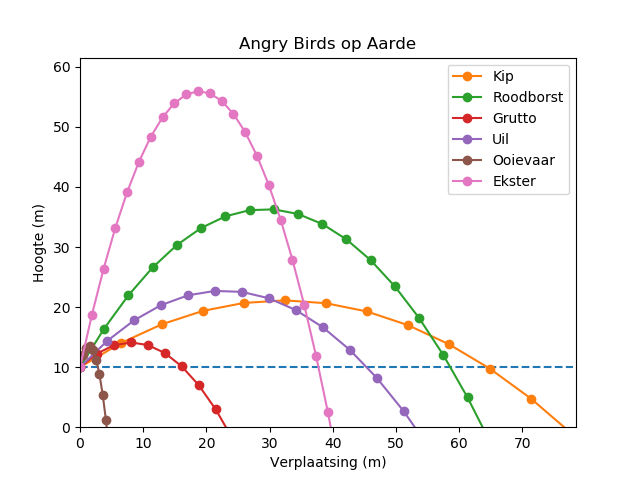
We verwachten dat er bij de implementatie van de verschillende AngryBirds functionaliteiten goed gebruik is gemaakt van functies. Met goede, generieke en geparametriseerde functies voor het berekenen van de data, het lezen van bestanden en het maken van de plots kunnen een hoop regels bespaard worden! Het is ook toegestaan om een klasse AngryBirds te maken waarin de data (vogels, planeten) wordt opgeslagen en de benodigde functionaliteiten rond die data zijn geïmplementeerd.

Verslag

We verwachten een verslag (uiteraard weer in LaTeX) dat het volgende bevat:

  1. Een korte omschrijving van het programma.
  2. Een beschrijving van punten waarop het programma faalt (indien van toepassing)
  3. Een tabel met gewerkte uren (per week en per persoon).
  4. Een klein onderzoekje waarin een interessante Life-configuratie (bijvoorbeeld van internet; uiteraard met een nette citatie = referentie ("\cite") en twee plaatjes met screenshots van het eigen programma) wordt bestudeerd.
  5. Een interessante plot van Angry Birds. Kies zelf een planeet of vogel. Je mag de "standaard"-vogels gebruiken, of zelf een lijstje vogels afvuren. Experimenteren met andere planeten mag ook! Ook hier weer een korte discussie over iets dat je opviel of interessant is. Om de plots in PDF-formaat in het verslag te plaatsen kun je gebruik maken van de graphicx-package, zie ook het elfde werkcollege.
  6. Voeg de Python code toe door gebruik te maken van LaTeX listings. Graag elk bestand in een aparte sectie en zorg dat het duidelijk is wat de naam is van elk bestand.

Opmerkingen & Tips

  • Zeer ruwe indicatie voor de lengte van het Python-programma, inclusief infoblokje, witregels en commentaren: 500 - 650 regels. Op hoeveel regels je uitkomt is natuurlijk afhankelijk van de mate van commentaar en gebruik van witregels.
  • Hoe kunnen we zien of het omzetten naar een int (bijvoorbeeld voor menukeuzes) goed gaat? 
    geldige_keuze = True
try:
    keuze_als_int = int(ingevoerde_keuze)
except ValueError:
    geldige_keuze = False
  • Ter inspiratie een beginnetje van een klasse LifeWereld: 
    class LifeWereld(object):
    '''Bevat alle data van de huidige wereld en methoden om een nieuwe
    generatie uit te rekenen en de wereld aan te passen.'''
    def __init__(self, hoogte, breedte):
        self.hoogte = hoogte
        self.breedte = breedte
        self.generatie = 0

        self.kar_levend = 'x'

        self.wereld = np.zeros( (..., ...), dtype=np.bool8)
        # enz ...

    def afdrukken(self):
        '''Drukt de wereld af naar standard output.'''
        pass

    def schoon(self):
        '''Verschoon de wereld: alle cellen worden gedood.'''
        pass

    def random(self):
        pass

    def plaats_glider(self, rij, kolom):
        '''Plaats een glider op positie (rij, kolom); dit is de linkerbovenhoek
        van de glider.'''
        pass

    # TODO: enzovoort

Inleveren

Uiterste inleverdatum: maandag 4 december, 17:00 uur vrijdag 1 december, 17:00 uur


Manier van inleveren:

  1. Digitaal zowel de Python-code (de .py-bestanden gebundeld in een .zip of .tar.gz bestand) als het verslag (in PDF-formaat). Inleveren via BlackBoard. Onder "Content / Course Documents" vind je een onderdeel "Opdracht 3". Geef de bestanden bij voorkeur de namen sXXXXXXX-sYYYYYYY-opdr3.zip (of sXXXXXXX-sYYYYYYY-opdr3.tar.gz voor .tar.gz bestanden) en sXXXXXXX-sYYYYYYY-opdr3.pdf met op de plekken van XXXXXXX en YYYYYYY de studentnummers van de makers ingevuld. Als dat niet lukt, is het ook prima alle Python-bestanden als losse attachments op te sturen. Gebruik geen spaties in de bestandsnamen. .pyc-bestanden hoeven niet te worden meegestuurd. De laatst voor de deadline ingeleverde versie wordt nagekeken.
  2. En ook een papieren versie van het verslag (inclusief alle Python-code) deponeren in de speciaal daarvoor bestemde doos "Programmeermethoden NA (Python)" in de postkamer van Informatica, kamer 156 van het Snellius-gebouw.
    Overal duidelijk datum en namen van de twee makers vermelden, in het bijzonder als commentaar in de eerste regels van de Python-bestanden.

Te gebruiken interpreter: Python 2.7.
Het programma moet in principe zowel op een Linux-machine, als onder Mac en Windows draaien. Zorg in ieder geval dat het programma werkt op de computers van de universiteit.

Normering: layout 1; verslag en commentaar 2; modulariteit (OOP, functies) 2; werking 5.