Data Fusion:
A Way to Provide
More Data to Mine in?
Peter van der Putten
ab
a Sentient Machine Research
Baarsjesweg 224,
1058 Amsterdam, The Netherlands
pvdputten@smr.nl
Abstract
In everyday data mining practice, the availability of data is often a serious problem. For instance, in database marketing elementary customer information resides in customer databases, but market survey data is only available for a subset or even a different sample of customers. Data fusion provides a way out by combining information from different sources for each customer. We present a simple data fusion procedure based on a nearest neighbor algorithm. We suggest different measures to evaluate the quality of the fusion process. An experiment on real world data is described to illustrate the added value of our approach.
1.
Introduction
and motivation
In marketing, direct forms of communication are
getting more popular. Instead of broadcasting a single message to all customers
through traditional mass media such as television and print, the most promising
potential customers receive personalized offers at the most appropriate time
and through the most appropriate channels. So it becomes more important to
gather information about media consumption, attitudes, product propensity etc. at
an individual level.
The amount of data that is collected about
customers is generally growing very fast, however it is often scattered among a
large number of sources. For instance, elementary customer information resides
in customer databases, but market survey data depicting a richer view of the
customer is only available for a small sample. Simply collecting all this
information for the whole customer database in a single source survey is often
too expensive.

Figure 1: Data Fusion in a nutshell
A widely accepted alternative within database
marketing is to buy external socio-demographic data that has been collected at
a regional level. All customers living in a
single region, for instance in the same zip
code area, receive equal values. However, the kind of information that can be
acquired is relatively limited. Furthermore, the assumption that all
customers within a region are similar is at the least questionable.
Data fusion techniques can provide a way out.
Information from different sources is combined by matching customers on
variables that are available in both data sources. The resulting enriched data
set can be used for all kinds of data mining and database marketing analyses.
In this paper we will give a practical
introduction to the application of data fusion for data mining in a database
marketing context (section 2). This will be illustrated with some preliminary
empirical results on a real world data set (section 3). Rather than presenting
a complete solution we argue that data fusion might be a valuable tool in every
day data mining practice. Furthermore we aim to demonstrate that the data
fusion problem is far from simple and contains a lot of interesting topics for
future algorithmic and methodological data mining research (section 4).
2.
Data
fusion
Data fusion is not new. From the 1970s through
the 1990s the subject was quite popular, most particularly in the field of
media research [1,2,4,5,7,16] and micro economic analysis [3,10,11]. Up until
today, data fusion is used to reduce the required number of respondents or
questions in a survey. For instance, for the Belgian National Readership survey
questions regarding media and questions regarding products are collected in 2
separate groups of 10.000 respondents and fused into a single survey thus reducing
costs and time for a respondent needed to complete a survey [9].
In our research we are ultimately aiming at
fusing entire customer databases with surveys instead of merging surveys with
surveys. This implies new ways to exploit existing survey data. Furthermore,
the single source alternative - asking all the questions to all the customers -
might be an option for merging surveys, but in most cases it will not even be a
possibility when merging large customer databases with survey data.
2.1
Data
fusion concepts
The core data fusion concept is illustrated in
figure 1. Assume a company has one million customers. For each customer, 50
variables are stored in the customer database. Furthermore, there exists a
market survey with 1000 respondents, not necessarily customers of the company,
and they were asked questions corresponding to 1500 variables. In this example
25 variables occur in both the database and the survey: these variables are
called common variables. Now assume
that we want to transfer the information from the market survey, the donor, to the customer database, the recipient. For each record in the
customer database the data fusion procedure is used to predict the most
probable answers on the market survey questions, thus creating a virtual survey
with each customer. The variables to be predicted are called fusion variables.
The most straightforward procedure to perform
this kind of data fusion is statistical
matching, which can be compared to k-nearest neighbor classification. For
each recipient record those k donor
records are selected that have the smallest distance to the recipient record,
with the distance measure defined over the common variables. Based on this set
of k donors the values of the fusion
variables are estimated, e.g. by taking the average for ordinals or the mode
for nominals.
Sometimes separate fusions are carried out for
groups for which 'mistakes' in the predictions are unacceptable, e.g.
predicting 'pregnant last year' for men. In this case the gender variable will
become a so-called cell variable; the
match between recipient and donor must be 100% on the cell variable, otherwise
they won't be matched at all.
2.2
Data
fusion evaluation
An important issue in data fusion is measuring
the quality of the fusion; this is far from straightforward.
The bottom line evaluation is what we call the
external evaluation. Assume for instance that we want to improve the response
on mailings for a certain set of products, so this was the reason why the
fusion variables were added in the first place. In this case, one way to
evaluate the external quality is to check whether an improved mail response
prediction model can be built when fused data is included in the input.
However, the added value of socio-demographic and other external variables is often
of limited value for purely predictive modeling. These variables have more
value for descriptive data mining, e.g. discovering why people are interested
in these products [13,14]. The added value of the fused database is that
associations can be determined between variables that are unique for the
customer database and fusion variables from the market survey.
The internal evaluation of the data fusion
procedure is simply the a priori evaluation before external evaluation has
taken place. We identify evaluating representativeness versus predictiveness,
although the problem to make this distinction formal is an interesting problem
on its own. One challenge for both the fusion procedure and the evaluation of
representativeness of the fused data is that the donor and the recipient might
be samples from different populations, e.g. a customer database from a bank
versus a national media survey. If both donor and recipient are samples from
the same population, penalty factors can be used to punish ‘popular’ donors to
ensure that donors are used evenly and joint distributions between commons and
fusion variables are retained [11]. The penalty factor is popularity measure
that is added to the distance measure. Standard statistical tests can be used
to check whether there are significant deviations in frequency distributions
for variable values in the fused data set. An interesting problem when testing
predictiveness is that in general there are no target values available for the
recipient, so measures like root mean squared error and classification error
can generally only be calculated for the donor.
3.
Experiments
& results
In this section we will describe some
preliminary experiments and results with a standard statistical matching data
fusion procedure. We assume the following hypothetical business case. A bank
wants to learn more about its credit card customers and expand the market for
this product. Unfortunately, there is no survey data available that includes
credit cardholdership, this variable is just known for actual customers. Data
fusion is used to enrich a customer database with survey data; we assume that
donor and recipient are random samples from the same population.. The resulting
data set serves as a starting point for further descriptive and predictive data
mining analysis.
3.1
The
data sets and fusion methodology used
To approximate the bank case we did not use separate donors, but we chose to split up an existing real world market survey into a donor and a recipient. The recipient contained 2000 records with a cell variable for gender, commons for age, marital status, region, number of persons in the household and income. Furthermore the recipient contained a unique variable for credit card ownership, the target variable to model. The donor contained 4880 records, with 36 variables for which we expected that there might be a relation to credit cardholdership: general household demographics, holiday and spare time activities, financial product usage and personal attitudes. The original survey contains over a thousand of variables and over 5000 possible variable values.
We fused the donor and the recipient using 4 fold cross validation on the donor to determine the optimal k based on root mean squared error. Only ordinals and binary fusion variables were included, so we restricted ourselves to predicting averages.
3.2
Internal
evaluation: representativeness
Apart from the root mean squared error cross
validation procedure we restricted ourselves to representativeness evaluation.
First we compared averages for all variables
for the donor and the recipient. As could be expected from the donor and
recipient sizes and the fact that both sets were generated from the same source
there weren't many significant differences between donor and recipient for the
common variables. Within the recipient 'not married' was over represented
(30.0% instead of 26.6%), 'married and living together' was under represented
(56.1% versus 60.0%) and the countryside and larger families were slightly over
represented. The average fusion variable values were very well preserved in the
recipient survey compared to the donor survey. Only the averages of "Way
Of Spending The Night during Summer Holiday" and "Number Of Savings
Accounts" differed significantly, respectively by 2.6% and 1.5%.
Apart from general statistics we wanted to
evaluate the preservation of relations between variables, for which we used the
following weak measures. For each common variable we listed the correlation
with all fusion variables (the real values for the donor and the predicted
values for the recipient). The mean difference between common-fusion
correlations in the donor versus the recipient was 0.12 ± 0.028. In other
words, these correlations were very well preserved. A similar procedure could
be carried out for the fusion variables with respect to each other. Further
work should also be done on the application of penalty factors to improve
representativeness. However, our preliminary experiments have demonstrated that
penalties have a negative effect on the prediction quality (measured in rmse).
3.3 External value of fused data for prediction tasks
To experiment with the added value of data fusion for further analysis (external evaluation) we first performed some descriptive data mining to discover relations between the target variable, credit cardholdership, and the fusion variables using straightforward univariate techniques. First we selected the top 10 fusion variables with the highest absolute correlations with the target (see Table I). Note that, in contrast to standard practice, it is perfectly allowed to include fusion variables such as ‘frequency usage credit card’ in the set of input variables for prediction, because these variable values were based on predictions on the common variables. Smaller effects included "Need for cognition" (average 1.05 times higher) and less "housewives" (0.9 times lower). These results can already offer a lot of insight to a marketer. Also, when new products launched, the relation with survey variables can be estimated without carrying out a new survey.
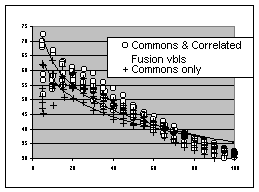
The descriptive results were also used to guide the predictive data mining modelling process. In this case we wanted to investigate whether different computational learning methods would be able to exploit the added information in the fusion variables. We included neural networks, linear regression, k nearest neighbor and an adapted version of Naive Bayes adapted for ordinals (Naive Bayes Gaussian). We report results over 10 runs with train and test sets of equal size. The quality of the models was measured by the so called c-index, a rank based non parametric test related to Kendall's Tau [12], which measures the concordance between the ordered lists of real and predicted cardholders (see [15] for details on the algorithms and the c-index).
We compared models trained on commons only, for which no fusion was actually needed, and models on commons plus either all or a selection of correlated fusion variables (see Table II; c=0.5 means random prediction, c=1 means perfect prediction). These results indicate that for this data set the models that include the fusion variables outperform the models built using commons only. For linear regression these differences were most significant. Significance was tested by a one sided two sample T test on the ‘fusion’ runs versus the ‘only commons’ runs. In figure 2 cumulative response curves are drawn for the linear regression models. The test recipients are ordered from high score to low score on the x-axis. The data points correspond to the actual proportion of cardholders up to that percentile. Random selection of customers results in an average proportion of 32.5% cardholders. Credit cardholdership can be predicted quite well: the top 10% of cardholder prospects according to the model contains around 50-65% cardholders. The added logarithmic trend lines indicate that the models which include fusion variables are better in 'creaming the crop', i.e. selecting the top prospects.