Deze tekst is verschenen in Eureka!, jaargang 1, nr. 4, december 2003, pp. 5-7. Eureka! is een uitgave van de stichting IMPACT en wordt vier keer per jaar gratis verspreid onder studenten en wetenschappelijk personeel van de opleidingen Informatica, Natuurkunde, Sterrenkunde en Wiskunde aan de Universiteit Leiden. De stichting IMPACT werkt voor Eureka! samen met studievereniging De Leidsche Flesch.

Walter Kosters, Informatica, Universiteit Leiden.

NP-volledigheid en Tetris

Houdt zij/hij van mij? Dat is een ja-nee vraag die velen van ons bezig houdt. En nog zoiets: heb ik de Postcode-kanjer gewonnen? Stel je voor dat een vriend tegen je zegt dat dat laatste het geval is: ja, ik heb de Postcode-kanjer gewonnen - een miljoen euro. Je vertrouwt het niet zo, en vraagt om bewijs. Hij laat een giro-strookje zien en een video van een bezoek van een BN-er. Inderdaad, echt waar, een miljoen gewonnen. Lastiger is het als hij zegt dat hij niet een miljoen gewonnen heeft. Lastiger omdat dat moeilijker te bewijzen is. Hoe kun je inzien dat iemand niet een miljoen euro gewonnen heeft? Een manier zou zijn om bij alle huizen in Nederland aan te bellen, net zolang tot je ergens te horen (en te zien) krijgt dat daar de prijs is gevallen, en dat dat niet het huis van je vriend is. Maar dat kost afschuwelijk veel tijd.

Nu maar meteen exacter. Er zijn ja-nee problemen, waarvan een ja-antwoord relatief eenvoudig te controleren valt. Laten we maar eens naar grafen kijken: een stel knooppunten, onderling verbonden door een stel takken. Dat een graaf een Hamilton-circuit toelaat, dat wil zeggen een wandeling langs alle knopen (zonder een knoop of tak twee maal te bezoeken - behalve de eerste knoop, die ook de laatste moet zijn), is eenvoudig te controleren als iemand je zo'n circuit laat zien. Hij of zij geeft eigenlijk een (kort) bewijs van de bewering: er is een Hamiton-circuit, namelijk van die naar die, en dan zo, etcetera. Als een graaf geen Hamilton-circuit (b)lijkt te hebben wordt dat doorgaans moeilijker: er is geen kort efficient algoritme bekend dat dit probleem oplost. Er is wel een rechttoe rechtaan bewijs dat in zekere zin simpel is: probeer maar alle mogelijkheden, en doe steeds een eenvoudige controle. Simpel, maar zeer tijdrovend. Het is daarom niet eenvoudig om iemand ervan te overtuigen dat een flink ingewikkelde graaf geen Hamilton-circuit heeft. Helaas - heel veel eenvoudig werk houdt je lang van de straat. Overigens, als de graaf toevallig een losse knoop heeft of slechts één verbinding tussen grotere eilanden, dan is het wel eenvoudig in te zien dat er geen Hamilton-circuit is - logisch dat je geen treinrondreis langs Europese hoofdsteden als Londen, Parijs en Amsterdam kunt maken.

  Graaf met Hamilton-circuit

De soort problemen waar we het hier over hebben heten wel NP-volledige problemen. Het zijn ja-nee problemen, waarbij het ja-gedeelte eenvoudig te doen is, maar waar voor de zogenaamde nee-instanties alleen bruut rekenwerk de nee-claim controleert. Tenminste, tot op de dag van vandaag. Het is niet uitgesloten dat iemand alsnog een efficient Hamilton-algoritme vindt, maar de meeste wetenschappers denken dat zo'n algoritme niet bestaat. Dat is het bekende "P verschilt van NP" vermoeden, waarvoor een grote financiële beloning klaar ligt voor de oplosser, zie hier.

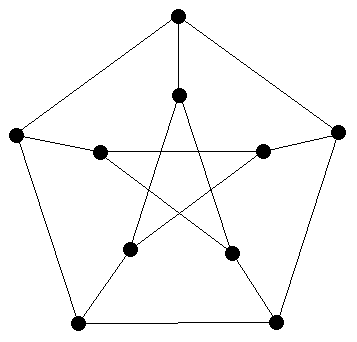  Graaf zonder Hamilton-circuit

Wat betekenen die P en die NP? De letter P staat voor polynomiaal, en slaat op ja-nee problemen die in polynomiale tijd op te lossen zijn. Zo'n probleem is bijvoorbeeld het beoordelen of een graaf al dan niet samenhangend is: kun je vanuit een knoop overal komen? Dit blijkt eenvoudig te beoordelen in polynomiale tijd. Polynomiaal in wat overigens? Als antwoord verwacht je niet alleen "in seconden", maar meer zoiets als "in de lengte van de invoer": je hoopt bijvoorbeeld een oplossing van je probleem te vinden in x-tot-de-derde seconden, als je probleem x bits had. Dat valt intuitief wel te billijken: in ons Hamilton-probleem van hierboven konden we prima een nee-instantie verifieren, alleen moesten we dan gigantische hoeveelheden wandelingen in de graaf controleren. En voor een veel grotere graaf accepteren we best een veel langere rekentijd - maar bijvoorbeeld niet exponentieel veel tijd.

En NP? Betekent dat niet-polynomiaal? Net niet: het bekent "niet-deterministisch polynomiaal". Zonder details te noemen, dit betekent dat je algoritme mag "gokken". En als nu geen enkele gok iets oplevert (informeel: geen enkel gegokt Hamilton-circuit "doet" het), hadden we blijkbaar een nee-instantie van ons probleem te pakken. In zekere zin kun je die problemen dus toch in polynomiale tijd oplossen, maar moet je daarvoor wel een "niet- deterministische" gok wagen. En normale bewijzen doen bijvoorbeeld al die gokken een voor een achter elkaar, en verstoken dan helaas veel te veel tijd.

Samengevat: er zijn problemen, de zogeheten NP-volledige, die naar ons huidige inzicht niet snel zijn op te lossen. En die problemen hebben een vreemde a-symmetrie: een ja-instantie is met behulp van een kort voorbeeld direct te controleren, voor een nee-instantie moet je erg hard werken en lang wachten. Het woordje "volledig" in NP-volledig slaat overigens op de moeilijkste NP-problemen, waar het Hamilton-probleem er een van is.

Wat heb je er aan als je weet dat een probleem NP-volledig is? Je weet dan in ieder geval dat het vinden van een eenvoudige exacte oplossingsmethode niet zal meevallen, en dat er misschien zelfs helemaal geen eenvoudige oplossing bestaat. En dat dus andere technieken wellicht te prefereren zijn, bijvoorbeeld methoden die benaderende antwoorden geven ("ze houdt 99% zeker van me"). En daar zijn er in de informatica vele van: genetische algoritmen en neurale netwerken, om maar wat categorieen te noemen.

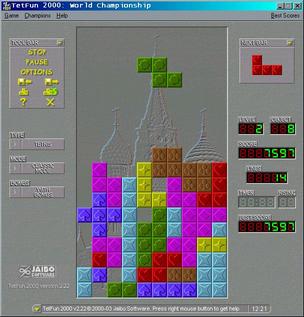  Tetris

Midden vorig jaar bewezen drie onderzoekers van het MIT in Boston dat Tetris NP-volledig was. Ruw samengevat: gegeven een serie Tetris-stukken, is het buitengewoon moeilijk om te beslissen of je daarmee een deels reeds gevuld Tetris-bord al of niet kunt leeg spelen. Een van onze studenten, Ron Breukelaar, slaagde er in -voor een project tijdens het afronden van zijn studie Informatica- hun bewijs sterk te vereenvoudigen. En dat leidde weer tot een gezamenlijk artikel van drie Leidenaren en de drie mensen van het MIT. Het bewijs brengt een bekend NP-volledig probleem in verband met het Tetris-probleem, een techniek die reductie genoemd wordt. Als je het ene probleem kunt oplossen, dan (via die reductie) ook het andere - dat is het idee.

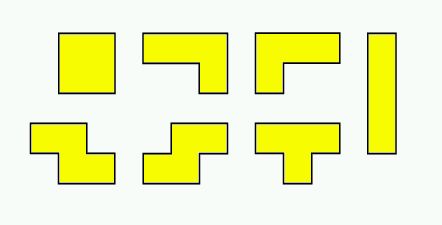  De 7 Tetris-stukken

Voor hen die Tetris niet kennen: koop een Gameboy, of kijk op het internet, waar ook veel over de geschiedenis van dit spel te vinden is. Simpel samengevat gaat het eenpersoonsspel als volgt. Er zijn 7 verschillende Tetris-stukken, elk uit 4 vierkante blokjes bestaand. Een voor een vallen dergelijke Tetris-stukken in willekeurige volgorde omlaag in een eerst leeg Tetris-bord, net zolang tot ze op een ander stuk stuiten of op de bodem. Als een rij helemaal gevuld is, verdwijnt deze rij. (De stukken erboven vallen er trouwens dan niet door heen, maar komen een rij lager.) De speler kan stukken roteren en horizontaal verschuiven. De bedoeling is om zoveel mogelijk stukken kwijt te raken, zonder het bord te laten "overlopen".

Tetris had meer te bieden dan NP-volledigheid. In het bovengenoemde artikel werden bepaalde constructies gebruikt, en de vraag was of die "in het wild" konden voorkomen. Het antwoord bleek ja te zijn: elke configuratie van vierkante blokjes kan verkregen worden, mits je de juiste stukken krijgt en die op de juiste manier laat vallen. In de praktijk, bij een echt potje Tetris, is dat anders: daar heb je geen controle over de stukken die je krijgt, alleen over de plek waar en de orientatie waarin je ze laat vallen - maar dat is hier even niet het punt. Het resultaat hier is: als de breedte van het bord oneven is, kun je elke configuratie maken, zie hier voor meer uitleg en een Java-animatie van het algoritme. Voor borden van even breedte is er een kleine technische conditie waaraan voldaan moet worden. Dat kun je eenvoudig inzien. Stel dat het bord bijvoorbeeld 8 breed is. Ieder Tetris-stuk dat erbij komt bestaat uit 4 blokjes, en als een rij wordt leeggespeeld verdwijnen er 8 blokjes. Conclusie: er is altijd een 4-voud aan vakjes bezet.

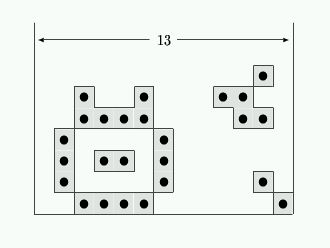  Deze configuratie kan verkregen worden met 276 geschikte Tetris-stukken

En van daaruit doemde de vraag op of je uberhaupt kon beslissen of bepaalde rijtjes Tetris-stukken (gegeven inclusief hun positie en orientatie) het bord schoon achterlaten. Voor een enkel rijtje is dat niet moeilijk: laat maar vallen die stukken, en kijk wat er gebeurt; maar als de rijtjes gegenereerd worden door een eenvoudige automaat, is de vraag of er ooit zo'n leuk schoon vegend rijtje bij zit opeens te moeilijk ... Dat blijkt namelijk al niet te kunnen als je alleen het "I-stuk" hebt. Kortom, een resultaat van een ander type. Het leuke is dat dit allemaal niet ons eigenlijke werk is, maar dat het wel leidt tot boeiende informatica ...

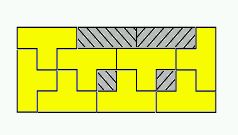  Hoe je met 10 "T-stukken" een 4 bij 10 bord leegt

Een aardig detail uit dat laatste stuk onderzoek is het volgende. Stel dat je alleen maar "T-stukken" hebt, en wel tien stuks, op een bord ter breedte 10. Je kunt laten zien dat er geen manier is om een horizontale 4 bij 10 vloer precies met 10 T-stukken te bedekken (een algemener geval bewees een wiskundige al in 1965). Maar in de Tetris-wereld kan het wel: je kunt de eerste 8 T-stukken zo laten vallen dat er een rij (zelfs twee) verdwijnt, en precies gaten voor de 2 resterende T-stukken overblijven.

Het blijft echter een probleem of de vraag "Houdt zij/hij van mij?" NP-volledig is. Lastig is het wel.

Met dank aan Hendrik Jan Hoogeboom, en aan de makers van enkele plaatjes (Förderverein Mathematik, Petersen graph en TetFun 2000).

Vragen en/of opmerkingen kunnen worden gestuurd naar: kosters@liacs.nl.

18 december 2003 - http://www.liacs.nl/home/kosters/tetris/teet.html