De derde programmeeropgave (in het voorjaar van 2019) behorende bij het vak
Kunstmatige intelligentie gaat over de twee-persoons
spellen Gomoku en Othello. Het is de bedoeling het minimax-algoritme, en ook het alpha-beta-algoritme,
te implementeren, voor een geschikte evaluatie-functie.
Op een rechthoekig m bij n bord bevatten de niet-lege
vakjes een witte of zwarte schijf.
Standaard-Othello is op een 8-bij-8 bord.
De beginstand kan willekeurig zijn, of juist regelmatig.
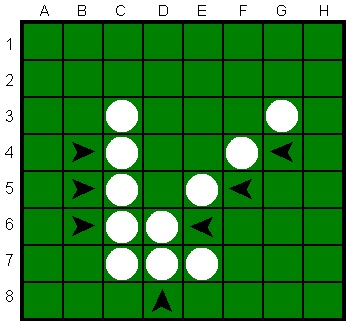
Bij Gomoku is het spelbord in het begin doorgaans leeg, bij Othello
is die zoals in het linker groene plaatje.
Als een speler aan de beurt is (ze spelen om en om)
moet hij/zij een steen van de eigen kleur plaatsen.
Bij Gomoku mag dit op ieder leeg vakje, bij Othello zodanig dat er "geslagen" wordt.
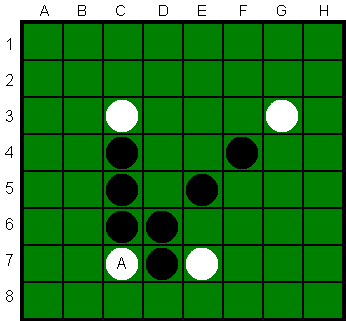
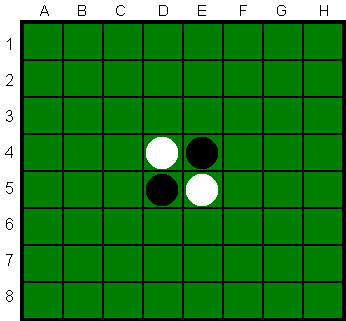
Dat laatste betekent dat er één of meer stenen van de tegenstander nu
direct ingesloten raken, horizontaal, verticaal of diagonaal; deze klappen allemaal om van kleur na het slaan (zie tweede en derde plaatje, na zetten op plek A).
Je wint bij Gomoku door 5 (of meer) stenen van de eigen kleur horizontaal,
verticaal of diagonaal naast elkaar te krijgeni; als het bord vol is,
en niemand er 5 naast elkaar heeft, is het remise.
Als je bij Othello niet kunt, moet je passen; als beide spelers
niet meer kunnen, stopt het spel, en wint degene met de meeste eigen stenen;
remise is hier ook mogelijk, namelijk als beide spelers evenveel stenen hebben.
Er is voorbeeldcode voor Gomoku beschikbaar, waarin diverse functies zitten om het spel te spelen, en zelfs een randomspeler, een "gretige links-boven speler" en een Monte-Carlo speler. En een template voor de minimax-speler. Elke speler zit in een eigen file. En ook voorbeeldcode voor Othello. De code stelt je in staat om twee verschillende spelers = programma's het spel tegen elkaar te laten spelen. Lees eerst het commentaar en bestudeer de meegeleverde spelers. Wijzig alleen daar waar in de code "TODO" staat. Doe bij voorkeur eerst Gomoku. En excuses voor het gebruik van Nederlands en Engels door elkaar.
Het is de bedoeling een zoekalgoritme te schrijven dat, gegeven een spelconfiguratie, een zo goed mogelijke zet vindt. We gebruiken hiervoor het minimax-algoritme, bij voorkeur met alpha-beta pruning. Er moeten verschillende (member-)functies geschreven worden:
De eerder genoemde functies mogen natuurlijk worden aangevuld met meer geavanceerde technieken of heuristieken zoals: quiescence search, null-moves, transpositie-tabellen, etc. Ook stellen we interessante evaluatie-functies op prijs (let op de executiesnelheid en rapporteer daarover; denk: circa een minuut voor tien tweepersoons spelletjes Gomoku, Monte-Carlo met MCSPELLEN (het aantal playouts) gelijk aan 200 tegen minimax met RESOURCES gelijk aan 100000, op een 10 bij 10 bord).
Een paar opmerkingen:
Deadline: donderdag 25 april 2019, 11:00 uur.
In te leveren: een geprint exemplaar van het verslag
(alleen eigen C++-code in de appendix)
tijdens
het college, en de C++-code van het programma naar onderstaand adres.
Het verslag moet aan verschillende
eisen voldoen.
Vragen en/of opmerkingen kunnen worden gestuurd naar: w.a.kosters@liacs.leidenuniv.nl.
27 maart 2019 — http://www.leidenuniv.liacs.nl/~kosterswa/AI/othgom2019.html