P systems with objects

Membrane Computing
Gheorghe Păun: Membrane Computing, an introduction. Natural Computing Series, Springer, 2002. ISBN: 3-540-43601-4 Pierluigi Frisco: Computing with Cells: Advances in Membrane Computing. OUP, 2009 ISBN: 0199542864	presentation (pdf) (Based on DLT'02 and WMC'02) H.J. Hoogeboom presentation (pdf) (seminar Models of Computation, Utrecht, 2012) too much slides, includes Petri Nets under maximal strategy P systems web page (Milano) VIEWS project (Leiden 2004-2009) Three Leiden PhD students presented a thesis (partially) in membrane computing. Pierluigi Frisco. Theory of Molecular Programming — Splicing and Membrane systems. Ph.D. Thesis, Universiteit Leiden, May 2004. Robert Brijder. Models of Natural Computation: Gene Assembly and Membrane Systems. Ph.D. Thesis, Universiteit Leiden, december 2008. repository Jun Wang 汪隽. Spiking Neural P Systems. Ph.D. Thesis, Universiteit Leiden, december 2011. repository / papers Thís page is devoted to inert (non-reactive) P systems, where computation is performed by communication, and by moving objects around the system. Simple and elegant.
P systems with Carriers
Introduced in: C. Martín-Vide, Gh. Păun, G. Rozenberg, Membrane Systems with Carriers, Theoretical Computer Science 270 (2002) 779-796. » rules (associated to region) for multiset x carrier v: attach: vx → [vx] detach: [vx] → vx carry in: [vx] → in 'move into a membrane within the present region' carry out: [vx] → out	H.J. Hoogeboom. Carriers and Counters: P systems with Carriers vs. (Partially Blind) Counter Automata. In: M. Ito and M. Toyama (Eds.) Developments in Language Theory, 6th International Conference, DLT 2002, Kyoto, Japan, September 18-21, 2002, Revised Papers. pages 140-151. Lecture Notes in Computer Science 2450, Springer Verlag 2003. abstract: P systems with carriers are shown to be computationally complete with only one membrane and two carriers. We argue that their power is due to the maximal parallelism required in the application of the rules. In fact, with a single carrier, these systems are equivalent to partially blind counter automata. Finally, with a single passenger restriction the systems are again computationally complete. nb. partially was added to be slightly more in line with usual terminology! N·CP_m(c,p), where the parameters represent the number of membranes, carriers, and passengers per carrier, respectively. Theorem 1. N·RE = N·CP₁(2,3) Corollary 4. N·BC = N·CP_(1,) = N·CP₁(1,3) Theorem 5. N·RE = N·CP_(,1)
(12.1'05)	There is some recent interest in clockless P systems, i.e., systems without maximal parallellism. We quote a relevant part of the introduction: "The real value of our construction is that it suggests that the key feature of P systems responsible for universality is the requirement of maximal parallelism, that is, a computational step is illegal if it can be extended by applying another rule to objects not yet involved in the step. To support this conjecture, we show in Section 4 that carrier P systems that do not require maximal parallelism in their computational steps can be simulated by a blind counter automaton, i.e., a counter automaton unable to perform zero tests. This makes the situation similar to Petri nets, where adding maximal parallelism also gives universality [Bu81]. In the single carrier case there is no room for parallelism and we characterize the languages of single carrier systems as the partially blind counter languages, Corollary 4."

	Y. Gao, H.J. Hoogeboom. P Systems with Single Passenger Carriers. International Journal of Foundations of Computer Science 17 (2007) 1227-1235. doi:10.1142/S0129054107005273 abstract: Membrane systems with carriers holding only a single passenger are known to be computationally complete, although this result does not bound the number of membranes and the number of carriers. We show that actually two membranes suffice. Theorem 2. N·RE = N·CP₂(*,1)
P systems with Symport/Antiport
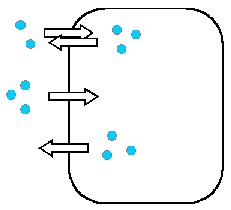
Introduced in: A. Păun, Gh. Păun. The Power of Communication: P Systems with Symport/Antiport. New Generation Computing, 20 (2002), pages 295-305. rules (associated to membrane) for multisets x,y: symport: (x,in), (x,out) antiport: (x,in;y,out)	P. Frisco, H.J. Hoogeboom. Simulating counter automata by P systems with symport/antiport. In: Membrane Computing: International Workshop, WMC-CdeA 2002, Curtea de Argeş, Romania, August 19-23, 2002. Revised Papers. Lecture Notes in Computer Science 2597, Springer Verlag 2003. abstract: The complexity, expressed in number of membranes and weight of rules, of P systems with symport/antiport generating recursively enumerable sets is reduced if counter automata instead of matrix grammars are simulated. We consider both subsets of N obtained by counting objects in a designated membrane, and string languages obtained by following the traces of a designated object. P systems with Symport/Antiport Theorem 3. N·RE = N·PP₁(sym₁,anti₂) Theorem 5. N·RE = N·PP₂(sym₃,anti₀) A single membrane suffices with 13 additional symbols in the output membrane. Theorem 9. N·RE = N·PP₄(sym₂,anti₀) Following the Traces ℓ is the size of the alphabet. Theorem 11. ℓ·RE = ℓ·PP_ℓ+1(sym₀,anti₂) = ℓ·PP_ℓ+1(sym₃,anti₀) = ℓ·PP_ℓ+2(sym₂,anti₀) Numbering of results as in the full paper: P. Frisco, H.J. Hoogeboom, P systems with symport/antiport simulating counter automata. Acta Informatica 41 (2004) 145-170. doi: 10.1007/s00236-004-0154-y
postscriptum 28.10'04	F. Bernardini and M. Gheorghe use new ideas for minimal symport/antiport to show that N·RE = N·PP₉(sym₁,anti₁), see their paper at the Workshop on Membrane Computing; Tarragona, July 17-22 2003.
postscriptum 4.1'06	A. Alhazov, M. Margenstern, V. Rogozhin, Yu. Rogozhin, S. Verlan bring the number of membranes down to three, after intermediate results by others: «Communicative P Systems with Minimal Cooperation», WMC 2004, Milano June 14-16, 2004, LNCS 3365, 2005.
	Overview and further ramifications are given in: A. Alhazov, R. Freund, Y. Rogozhin; «Computational Power of Symport/Antiport: History, Advances, and Open Problems», WMC 2005, Vienna, Austria, July 18-21, 2005, LNCS 3850, 2006 (pages 1 - 30) doi 10.1007/11603047_1
up up²

Membrane Computing

P systems with Carriers

P systems with Symport/Antiport