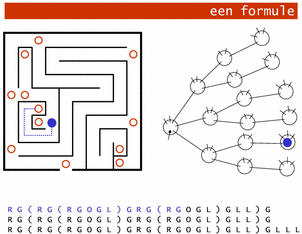
Een Formule voor Doolhoven?
UP "Waar is Hier de Uitgang?"
(Algoritmen in het Doolhof)

Applet Maze Solver
(demo depth-first search)


('simulatie' van de formule)

Ben, journalist van TRiV' "het maandblad voor nieuwsgierige mensen", belde in verband met zijn artikel over doolhoven. Hij vroeg onder andere: `bestaat er formule waarmee je uit elk doolhof kunt komen?'. Ik antwoordde dat zoiets niet bestond, dat je een kaart nodig hebt, of een manier om de gepasseerde gangen te markeren. Zo leg ik het uit bij mijn college wanneer we algoritmen op grafen behandelen.

Toch bleef de vraag intrigeren, en samen met buurman Walter ben ik er achter gekomen dat zo'n formule wel degelijk bestaat. Er is een recept waarmee je uit elk doolhof kunt komen, zonder kaart, touw, kiezelstenen of krijtje. In eerste instantie is de oplossing eenvoudig: probeer vanaf je uitgangspunt achtereenvolgens alle mogelijke paden, en keer tussendoor steeds terug. Omdat het recept voor alle doolhoven moet werken, weten we helaas niet hoe ver we door moeten lopen naar de uitgang. We weten dus niet hoe diep we moeten zoeken, en gaan daarom steeds dieper het doolhof in. Anderzijds weten we ook niet hoeveel keuzes er maximaal op een kruispunt van paden zullen zijn. We weten ook niet hoe breed onze zoektocht moet zijn, en voeren steeds meer keuzes per kruispunt in.

Het is slim om bij je wandeling door het doolhof gebruik te maken van de kennis die je onderweg opdoet. Maar we presenteren hier een 'domme' oplossing, om twee redenen. Allereerst gaan we ervanuit dat je de gangen en kruispunten niet noodzakelijk hoeft te kunnen onderscheiden. Als alles op elkaar lijkt kan de formule ook geen rekening houden met het aantal keren dat je ergens geweest bent. Dan zou je nog kunnen gebruiken dat je op een kruispunt van vier wegen niet zeven keer een gang hoeft te proberen. Dat doen we niet. We willen één formule, en die zal ook moeten werken bij zeven of meer gangen op een kruispunt. Daar betalen we voor dat er veel herhaling in onze zoektocht zal gaan zitten.

Hoewel we de kruispunten niet kunnen onderscheiden, doen we wel een andere aanname over de kruispunten. Het moet mogelijk zijn om uitgaande van een gang, de gang aan de linker of rechter hand te bepalen. In de praktijk geen probleem, maar als het doolhof drie dimensionaal is ligt dat niet voor de hand. We hebben dan een nummering van de gangen op elk kruispunt nodig. 

// HJH 21.3'07
// doolhof formule recursief
#include <iostream>
#include <string> 
using namespace std;

string phi ( int diepte )
{ 
  int i;
  string res = "", rec = "", suf;
  if (diepte == 0)  { return "O ";  }
  else
  {  
    rec = phi( diepte -1);
    for (i=1; i<= diepte; i++)
    { res += "R G " + rec + "G ";
      suf += "L "; 
    }
    return "( " + res + suf + ") ";
  }
}

int main ()
{ 
  int aantal = 3;
  cout << phi( aantal ) << endl ;
} // main

De formule

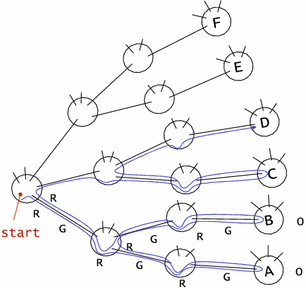
De eerste stap van onze formule is eenvoudig. We staan bij op het eerste kruispunt. We kiezen de gang aan onze rechterhand, en gaan die door naar het volgende kruispunt. Deze 'speurtocht' is één diep en ook één breed. Als recept is dat: rechtsaf, gang door, omdraaien op kruispunt, gang door, linksaf. We zijn dan terug op onze uitgangspositie. Een formule daarvoor zou kunnen zijn: R G O G L

Omdat het onmgelijk is dat we op dat ene kruispunt de uitgang vinden voor alle doolhoven, gaan we verder in de tweede stap, twee breed en twee diep. Vanuit de uitgangspositie gaan we twee gangen in en volgen die tot een tweede kruispunt. Vanuit dat kruispunt doen we elk nog een gang naar een volgende kruising, en keren steeds terug naar de basis. Het recept is dan: rechtsaf, gang door, rechtsaf, gang door, omdraaien, gang door, linksaf, gang door, [we zijn nu op de startpositie, kiezen de volgende gang en herhalen het recept voor die gang] rechtsaf, gang door, rechtsaf, gang door, omdraaien, gang door, linksaf, gang door. Als we precies bij de gang willen staan waar we vandaan kwamen, moeten we nu de tweede links zoeken. Dat is niet belangrijk voor de startkruising, maar wel als we het recept verderop in het doolhof gaan toepassen. Als we daar een formule voor willen: R G R G O G L G R G R G O G L G L L.
Er vallen ons twee dingen op. De formule herhaalt hetzelfde recept twee keer, voor opeenvolgende gangen vanuit de startpositie, door steeds de volgende rechtsaf te slaan (de blauwe R ). Ook zien we het eerste recept terug, de rode letters. Dat komt omdat we als we één diep in het doolhof zitten, we het eerste recept gebruiken om nog een nivo dieper te komen. We maken we wiskunde van en geven de formules een naam, φ, de griekse letter fi. De eerste fi-een, φ1 = R G O G L; voor fi-twee, de tweede, gebruiken we de eerste, en schrijven we φ2 = R G φ1 G R G φ1 G L L.

uitgeschreven: φ3  = R G ( R G ( R G O G L ) G R G ( R G O G L ) G L L ) G R G ( R G ( R G O G L ) G R G ( R G O G L ) G L L ) G R G ( R G ( R G O G L ) G R G ( R G O G L ) G L L ) G L L L Voor de derde stap zoeken we drie gangen elk drie diep door: rechts, gang door, tweede recept [dat ons netjes bij de positie brengt waar we de kruising binnenkwamen], gang door [we zijn weer terug], ... Dit herhalen we drie keer, en moeten dan de drie gangen naar links om de oorspronkelijke positie te vinden. φ3 = R G φ2 G R G φ2 G R G φ2 G L L L. Met wat fantasie kan dat korter, met de notatie voor machtsverheffen om herhaling aan te geven: φ3 = ( R G φ2 G )3 L3. Om deze manier laten de vierde en volgende stappen zich makkelijk opschrijven: φ4 = ( R G φ3 G )4 L4, etcetera. Dat elke formule uitgedrukt wordt in een vorige formule is een voorbeeld van recursie, een belangrijk begrip in de informatica.

De uiteindelijke oneindige formule die ons uit èlk doolhof brengt, is dan φ1 φ2 φ3 φ4 ... waarbij we doorgaan tot we de uitgang tegen komen. We zien dan de beginpositie en omringende kruispunten onnoemelijk vaak terug, steeds in grotere cirkels rondzoekend, steeds meer gangen per kruispunt proberend.

Herhaling

De formule beschrijft een steeds vertakkende wandeling. In het algemeen zitten er in een doolhof doodlopende gangen en rondlopende wandelingen, Dit zorgt voor extra herhalingen bij onze wandeling op zoek naar de uitgang. Elk eindpunt van een doodlopende gang wordt behandeld als een `kruispunt' met één gang. Elke opdracht (rechts, links, omdraaien) zorgt dat we die ene gang kiezen. We keren dan terug naar een kruispunt dat we al bezocht hebben. Voor de formule maakt dat niet uit. Elk kruispunt kan ofwel geheel vers zijn of een die we eerder bezochten. Dit geldt ook als we een kringetje hebben rondgelopen. De eerder bezochte knoop wordt behandeld als een nieuwe. De zoektocht wordt niet afgebroken (dat zou slim zijn) maar voortgezet. De reden is dat we een formule voor alle doolhoven willen opstellen.

Deze herhalingen ontstaan als we diep doorzoeken. Een andere bron van herhaling ontstaat als we op een kruispunt van zeg vier wegen, vijf of meer keer een gang ingaan. Ook dan doorzoeken we een gedeelte meerdere malen. Ook dit komt omdat we de preciese vorm van het doolhof waarin we ons bevinden niet willen gebruiken bij de zoektocht.

Plaatje: de zoektocht beschreven door φ3, in het ideale geval waarbij alle kruispunten verschillend zijn. Volg de blauwe lijn. Rechtsaf eerste pad volgen naar 'A' (R G R G R G) hier omdraaien en het pad terugvolgen twee kruispunten terug, daar rechts en door naar 'B' (O G L G R G R G) nu drie kruispunten terug naar het beginpunt (O G L G L L G) en rechtsaf naar 'C' (R G R G R G) dan naar 'D' net als eerder vanuit 'A' naar 'C' (O G L G R G R G) etcetera ... om uiteindelijk op het beginpunt drie gangen links gaan om bij de beginpositie te komen.